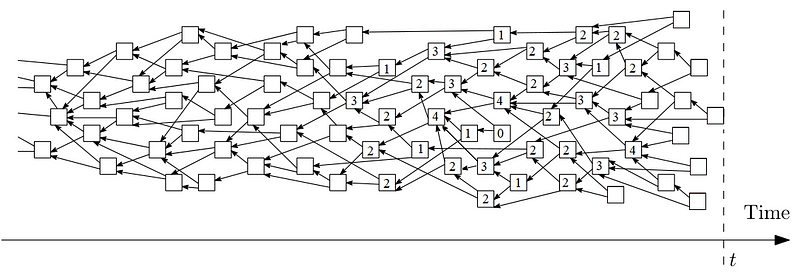
En este blog, hablamos sobre el número de aprobadores directos que puede recibir un tip. En la Tangle, cada transacción aprueba exactamente dos tips. Si bien esto implica que el número medio de aprobaciones directos es igual a dos, el número real de aprobaciones puede variar significativamente entre transacciones. Esto se muestra en la Fig. 1. Aquí veremos en particular la distribución de probabilidad P(n) para tener exactamente n aprobaciones. En otras palabras, estamos interesados en el número probable de caminos potenciales que un random walk escogerá de una transacción al azar. Esta métrica no sólo es interesante para investigar la estructura de la Tangle, sino que también nos permite hacer algunas predicciones probabilísticas. Por ejemplo, investigaciones recientes han demostrado que la distribución de probabilidad P(n) puede emplearse para predecir si ciertas partes de los ataques a la parasite chain tendrían éxito, lo que nos permite comprender en qué condiciones debemos aplicar la precaución.
En este blog, nos centraremos en la selección de tips con el random walk (recorrido aleatorio) de Markov-Chain-Monte-Carlo con el parámetro α puesto a cero. Aunque este valor no proporciona las mismas garantías de seguridad que el algoritmo de random walk con α más grande, sigue siendo útil para modelar la dinámica de la Tangle y puede proporcionar información útil para escenarios más genéricos. Además, en parte de este análisis también investigaremos el comportamiento de la Tangle cuando usemos una selección aleatoria uniforme de tips (URTS = uniform random tip selection). Esto nos permite obtener expresiones matemáticas más simples que aún reproducen algunas de las dinámicas.
La Fig. 2 muestra P(n) para URTS y α=0 si el algoritmo de selección de tips sólo crea enlaces simples. Por lo tanto, si se selecciona dos veces el mismo tip, sólo se crea una conexión entre el aprobador y el aprobado. Elegimos este enfoque, ya que es el más sencillo, y no debería afectar a los resultados en el régimen de alta carga si no hay tips dejados atrás. Puede ver que, con tipos de cambio bajos, es probable que una operación sólo tenga una aprobación (véase esto para más detalles). Por otro lado, a medida que λ aumenta, las probabilidades convergen hacia un valor constante. Note cómo para URTS la probabilidad de tener uno o dos aprobaciones es exactamente la misma, y que este no es el caso deα=0.

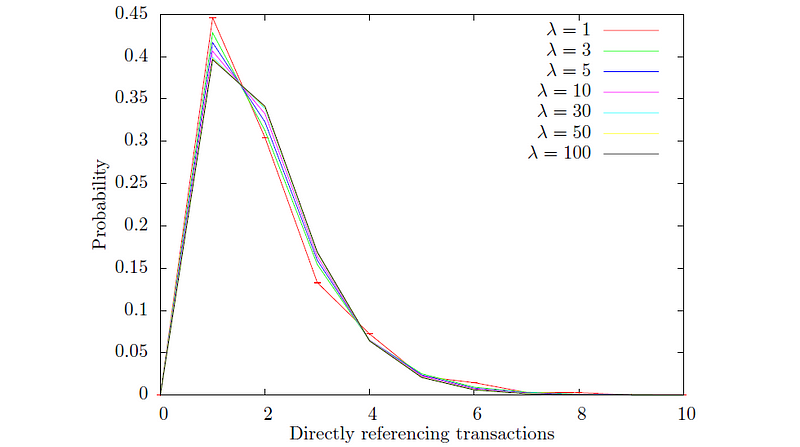
Podemos investigar esta distribución con más detalle. Se entiende bien que la distribución debe parecerse aproximadamente a una distribución de Poisson, lo cual se demuestra en la Fig. 3. Aquí podemos ver cómo se ve esta distribución y cómo depende de λ. Puedes notar que para todos λ la probabilidad de tener un alto número de aprobadores disminuye muy rápidamente. Podemos investigar esta distribución con más detalle. Se entiende bien que la distribución debe parecerse aproximadamente a una distribución de Poisson, lo cual se demuestra en la Fig. 3. Aquí podemos ver cómo se ve esta distribución y cómo depende de λ. Puedes notar que para todos λ la probabilidad de tener un alto número de aprobadores disminuye muy rápidamente.
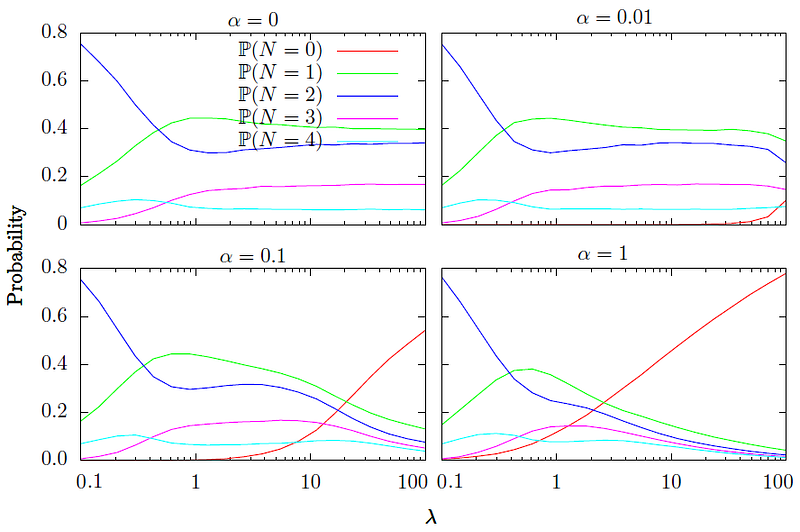
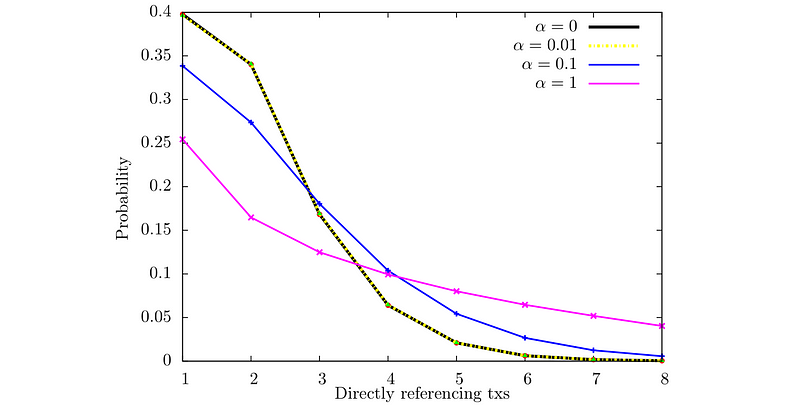
También podemos estudiar el comportamiento de la distribución para α>0, como se muestra en la Fig. 4. Puede ver que para cada α>0, a medida que aumenta la tasa de llegada λ, la probabilidad de que una transacción tenga cero aprobaciones se vuelve no despreciable. Sin embargo, podemos mejorar esta situación, por ejemplo, mediante la reimplantación de las transacciones o el ajuste de α adecuadamente. Para estos últimos, estudios como éste nos proporcionan información sobre dónde podemos colocar el parámetro.
Una vez que los tips se quedan atrás, la distribución P(n) y por lo tanto la estructura de la Tangle cambia. Para analizar este escenario, en la Fig. 5 se muestra la probabilidad de tener n aprobadores si se ignoran los tips dejadas atrás, es decir, no consideramos las transacciones con cero aprobaciones. Como se explica en la Fig. 4, el valor de α podría ser tal que el número de tips dejados no sea insignificante. En este caso se produciría un cambio sustancial en la estructura hacia un elevado número de enlaces para un número cada vez menor de operaciones aprobadas. En efecto, unas pocas transacciones se verían favorecidas sobre otras.
Como has visto, podemos aprender una cantidad significativa de información sobre la Tangle investigando las métricas mencionadas anteriormente. Sin embargo, hay más preguntas pendientes:
¿Cómo influye exactamente el parámetro α en esta distribución?
En caso de que cambiemos el valor de α a medida que la tasa de transacción cambia. Si es así, ¿cómo?
¿Cómo afecta exactamente a la distribución el número de tips dejados atrás?
¿Cómo afectan los reattachments esta distribución?
Esperamos poder mantenerle informado sobre los desarrollos que encontremos a medida que nuestra investigación avance en estos fascinantes temas. Como siempre, esperamos que hayan disfrutado del viaje a través de este aspecto de nuestra investigación y agradecemos sus comentarios y preguntas, ya sea aquí o en #tanglemath en nuestro Discord.
Artículo original: The structure of the Tangle — Number of approvers